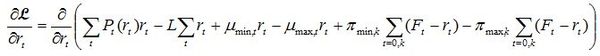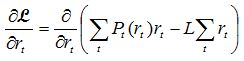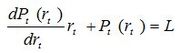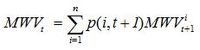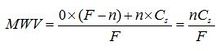EMK:Water Values and Hydro Offers

Disclaimer

Reasonable care has been taken to ensure that the information in this paper is up to date at the time of issue. Potential users of EMarket should, however, ensure that they evaluate EMarket and this paper through an appropriate evaluation process in consultation with Energy Link. The authors are also reliant on certain information external to EMarket and Energy Link, for which no liability or responsibility can be accepted.

Introduction

This technical bulletin is intended to provide users and interested parties with a detailed explanation of how EMarket’s water values are calculated and applied. EMarket was designed as a market simulation model rather than as an operational model and the algorithm developed by Energy Link for use in EMarket was designed to give a high degree of accuracy at high speed for this purpose. Speed of operation is a strength of EMarket and ensures that users can turn new or modified simulations around very quickly, achieving high levels of productivity.

EMarket is also a very flexible model which allows, for example, simulation runs to combine weekly, day-night and half hourly dispatches within one simulation run. This paper includes a brief overview of other features in EMarket.

Other Documents

This bulletin is one of a series of technical bulletins relating to Energy Link’s EMarket model. Taken together, the bulletins replace the old EMarket User Guide. The full series of bulletins covers an overview of the EMarket model, the details of the four major New Zealand hydro systems modelled in EMarket, water values and hydro offers, power flows, dispatch and nodal pricing, short term river chain optimisation and company optimisation.

Summary

The manager of a hydro system in New Zealand must deal with the prospect of uncertain inflows, concern about ensuring security of supply in a dry year, and how to maximise the value of water in the reservoir at any point in the year.

The concept of a marginal water value is useful in this context and defines the expected future value of the next cubic meter of water arriving in storage for generation. The water values calculated by EMarket and used in its full simulation runs are stored and viewed as water value contours, or curves of constant water value on a chart of storage versus time. Contour values are chosen to match the offer prices of thermal plant configured in each run.

EMarket’s water values have the following property: if the contour price is P_c then if the inflow scenarios entered into EMarket are projected forward using market dispatch with hydro offers at the constant value P_c, the number of scenarios that hit the bottom of the reservoir is equal to where F is the number of annual inflow scenarios entered into EMarket, N the security factor defined by the 1 in N security criterion used in New Zealand, and P the average nodal price for the simulation run.

If the water value is equal to and if F = N then the number of inflow scenarios which will hit bottom of the reservoir when projected forward using market dispatch and constant offer price , is equal to 1.

EMarket’s water values are calculated very quickly using a much simplified, weekly version of the full simulation run which does not use nodal dispatch and pricing. During the full simulation run the water values are adjusted using relative prices across the grid to ensure that the hydros offer their output at a price consistent with the optimum release at any particular time of year and storage value.

The offers of the major hydro systems modelled in EMarket can also be distributed optimally across injection nodes along their respective hydro systems, thus providing accurate modelling of nodal prices, losses and line constraints within and around the major hydro systems.

Water Values Defined

The concept of a water value is useful to the manager of hydro electric generation which has some storage because it tells the manager exactly how much the next MWh of generation is worth at any point in time. Knowing this, the manager could offer their hydro generation into a spot market, for example, at water value, and be dispatched more or less in order of offer price (The actual order depends also on the method used for dispatch. In New Zealand, and in many other electricity markets, nodal (or locational marginal) dispatch and pricing are used which also takes into account marginal losses and line constraints during dispatch).

Figure 1 - Water Value Contours as Operating Guidelines

Alternatively, if the manager operated an entire utility which had both hydro and thermal plant, then they could establish a place for the hydro in their "merit order", more simply the order in which the plant should be dispatched given its marginal cost of generation. The assumption here is, of course, that cheaper plant has more merit than expensive plant and should therefore be dispatched first.

Although we talk of water value, more correctly we should refer to marginal water value, which is defined as the expected future value of the next cubic meter of water arriving in storage for generation. This implies that the water value should be expressed, for example, in dollars per cubic meter of water. In practice, however, it is more convenient to express it in $/MWh of generation output.

Consequently, at any particular point in time, the hydro manager must decide if they use water in storage to generate now, or store it longer to use later. The hydro manager should take the opportunity to generate whenever the nodal price received for generation is equal to or exceeds the water value.

The marginal cost of thermal plant is made up of fuel and other variable costs of generation. Hydro electric plant has either small or negligible marginal costs, so the water value is effectively an opportunity cost – water used to generate now will not be available to generate later when we expect to obtain its current water value for generation from the hydro system.

Water Value Contours

The use of water value contours in EMarket arose from the useful concept of the operating guideline which in turn arose from the development of various models for ECNZ (Electricity Corporation of New Zealand) in New Zealand which owned most of the generation in the 1980s. An operating guideline is a curve on a chart of total storage for the reservoir in question versus time. The guideline establishes the hydro generator's place in the merit order at any given time of the year.

For example, the bold Huntly operating guideline shown in Figure 1, for any given time of year, gives the storage level at which the 1,000 MW Huntly power station should be operating, assuming a centrally planned system. At any time during the year Huntly should operate if storage is at or below the thick operating guideline shown. In practice, Huntly actually would come on progressively over a range of storage around the guideline. In addition, ECNZ's models calculated guidelines for all major thermal plant based on storage in the two islands, e.g. the other two guidelines shown relate to plant other than Huntly.

Another way to think of the operating guideline is a curve joining points of equal water value – in this case the average value of generation from Huntly.

Figure 2 - Typical water Value Contours for Waitaki

Thus, by definition, an operating guideline is a marginal water value contour. In designing EMarket, Energy Link decided to continue with the concept of an operating guideline because it is a useful way of visualizing how water value changes with storage and time. Water values can be represented in other ways but water value contours are highly visual and can be interpreted easily with only a little training.

The chart to the right shows typical water value contours for water in the big storage lakes of the Waitaki hydro electric system, Lakes Pukaki and Tekapo, as produced by EMarket. Each contour relates to the offer band from a thermal generator modeled in EMarket. At any given time in the year, if storage is exactly on a contour then it is obvious what it's water value is. If storage is between two contours then the water value is linearly interpolated between the two contours. For example, if storage is one third of the way between two contours of $50/MWh contour and $75/MWh, respectively, then the water value is simply .

New Zealand Major Hydro Systems

The four major hydro systems listed below are modelled in some detail in EMarket and water values are calculated for each major hydro system.

Waitaki

Major storage lakes Pukaki and Tekapo; inflows into lakes Pukaki, Tekapo, Ohau, and the Ahuriri River; eight power stations, some with smaller storage lakes immediately upstream.

Clutha

Major storage Lake Hawea; uncontrolled storage and inflows into lakes Wanaka and Wakatipu; other inflows from the Shotover River; Clyde and Roxburgh power stations each with small storage upstream.

Waikato

Lake Taupo with major inflows; eight power stations, each with small storage upstream, modeled downstream, of Taupo; five tributaries inflows modeled below Taupo.

Manapouri

Partially controlled storage Lakes Manapouri and Te Anau; power station at West Arm of Manapouri; outflows also down the Mararoa River.

Water values are also calculated for smaller hydro systems, e.g. Cobb and Coleridge hydro staions, if inflow data is available to EMarket.

Water Value Theory

Water value contours arise from the process of optimising the use of water in storage reservoirs upstream of one or more hydro power stations. In fact, the water value contours in EMarket allow the (simulated) hydro manager to calculate water values and simulated offers that are optimal, in a fast and convenient way.

The optimisation of a hydro generation scheme with seasonal storage is different to the optimisation of a thermal generator, which usually has access to fuel supply which effectively unlimited, for three main reasons:

1. the hydro "fuel supply," i.e. total inflows, is finite in any given year;
2. inflows into the storage reservoirs are highly volatile;
3. reservoir storage is finite.

There is one further constraint on hydro generation which is particularly important in New Zealand, where storage is relatively small compared to total inflows. The constraint is known as the "1-in-N" dry year security criterion, where N is in years. For example, the government's policy statement on electricity currently includes a 1-in-60 security criterion for dry year security of supply. In principle, this means that a shortage situation, in which demand curtailment becomes necessary or highly desirable, should only occur 1 year in 60, on average. The 1-in-N constraint is included in EMarket's water value calculations for each of the four major hydro systems modelled in EMarket.

We now ask the question - if a hydro station has operated for one year from time T₁, at which point it started out with storage of S₁, until time T₂ and storage of S₂, then what would have been its optimal set of releases at each point in the year?

The term release refers only to water released from storage to generate electricity, any other water leaving storage being classed as spill past one or more stations in the hydro system. In the following we make the assumption that generation is a constant function of release, measured in MW per cumec (1 cumec is 1 cubic metre per second). In fact, generation in MW is related to release in cumecs by a number that is approximately constant for most power stations, at least over a wide range of output. The curve relating output, g, to flow, f, through a hydro generator is given approximately by g = af - bf² where a and b are constants and the second order term in f represents frictional losses in the penstock feeding water to the turbine. In addition, a may vary with the operating head of the turbine as the lake level behind the hydro station varies – the head effect. In practice head effects are fairly small in the majority of hydro stations and usually insignificant for the purposes of the modelling undertaken with EMarket.

The time step used to calculate the water values is one week, so at some week t between T₁ and T₂ the revenue from release is given by:

[1]

where P_t is the generator's average weekly nodal spot price at time t. Total revenue for the year is given by:

[2] for all weeks between T₁ and T₂.

Marginal costs for hydro electric stations are very low, so if a hydro manager wishes to optimise gross profit over the year then they can just as easily optimise the revenue function R_tot.

A potentially important consideration is the effect of the release on the nodal price received at the node at which the generator injects, the magnitude of which may be significant if the hydro generator has market power. In practice, a higher release will often have a negative effect on the price, although for small amounts of generation this effect will usually be negligible. But to account for this possibility the nodal prices can be expressed as a function of release, P = P(r). The hydro revenue equation becomes:

[3] for all weeks between T₁ and T₂.

Figure 3 - Simple Hydro System

Before we can maximise revenue for the year we have to account for constraints on what we can achieve with our hydro electric system:

• maximum and minimum releases at each station downstream of the storage reservoirs;
• maximum and minimum storage in each reservoir;
• conservation of mass - at each step within the year the storage in any given reservoir increases by its inflows less releases and spill;
• minimum flow below stations, e.g. as set by resource consents or other conditions on the operation of each station;
• the specified 1-in-N dry year security criterion which states that the reservoir shall hit bottom only once on average in N years.

Working with a hydro system which consists of one reservoir and one station downstream, as shown in Figure 3, for the sake of simplicity, the constraints on the release are the maximum and minimum release:

[4] 0 ≤ r_t ≤ r_max for all t between T₁ and T₂

The constraints on storage are the maximum and minimum storage:

[5] for all t between T₁ and T₂

where f_t is the inflow at time t and S_min are S_max are the minimum and maximum storage.

The constraint on final storage is:

[6] for all t between T₁ and T₂

Deterministic Marginal Water Value

Using the method of Lagrange multipliers, assuming for the moment that inflows are known in advance (We refer to the inflows as deterministic rather than stochastic, the latter referring to uncertain inflows), and that we are clear of constraint conditions such as being at minimum or maximum storage, we now form the Lagrangian, , and differentiate for each r_t, which can be expressed as:

[7]

If all constraints except the binding constraint (conservation of water) given by [5] are ignored this becomes:

Equation 1: Simplified Hydro Lagrangian

[8]

This equation describes the optimal path in the absence of storage and generation capacity constraints. The remaining multiplier, L, is the marginal water value. Setting the partial derivatives of the Lagrangian to zero gives a result involving only a relatively simple differential equation:

[9]

for all t between T₁ and T₂, where L is a constant. Note that we can use the derivative of P_t rather than the partial derivative, since for our purposes P_t is a function only of r_t at each t.

Impact of Market Power

Figure 4 - Nodal Price vs Release with Market Power

It is worth noting here that dP/dr is always zero or negative and indicates the sensitivity of the market price at time t for a release of r_t. If the term is zero for all r_t then the hydro generator has no market power and is a pure price taker.

When a generator has market power then the curve relating nodal price to release might look like the complex curve shown below. The flat portion of the curve at medium and high values of r_t might represent a portion where the generator is on the margin, setting the price.

At the point shown where the tangent line intersects the curve, r_t has reduced to the point, effectively by reducing the amount offered into the market, where the generator is no longer on the margin and the price is being set by a higher priced generator. At this point, of course, dP/dr is the slope of the curve.

In the case of a generator exercising market power, it can then be concluded from the above equation that when the release is not constrained to a maximum or minimum the nodal price will be greater than the marginal water value. The r_t multiplier on the first term of our differential equation indicates that when the nodal price rises, release will be increased. If dP/dr is very small compared to P_t - the nodal price is minimally dependent on the release - then the nodal price will be more or less equal to the marginal water value and as such, constant over storage trajectories where release is not constrained.

This shows that optimal behaviour can be achieved by offering at a price that consists of a constant base price representing the marginal water value plus an additional price component that is added when nodal prices can be significantly raised by reducing release, i.e. by exercising market power.

Marginal Water Value Used in EMarket

In EMarket, the market power component of the water value equation is ignored when water value contours are calculated to give our result that hydro output should be offered each week at constant marginal water value, assuming deterministic inflows:

[10] P_t = L ≡ Marginal Water Value

In a more general sense, whether inflows are deterministic or stochastic, the marginal water value (often we refer to it just as the water value) gives us the expected future value of the next unit of water to be used to generate, given the assumptions we have made in order to derive them. In principle, the generator should generate while the price received for generation is at least the current marginal water value.

In this way, disregarding the use of market power at this stage, the behaviour of a hydro system can largely be determined by its current marginal water value. It is also worth reiterating at this point that that we are primarily concerned with the marginal value of water in long term storage reservoirs in each major hydro system. The value of water in smaller, intermediate reservoirs downstream of the long term storage reservoirs, at any point in time, could vary significantly from the value of water in the long term reservoirs - more on that in section 8.1.

Calculating Water Value Contours

To calculate water values, we must also model the reservoir manager's decision making process in the face of the considerable uncertainty about future inflows. Typically, decisions are made about the release of water from long term storage on a weekly basis. The reservoir manager knows current storage, the details of their reservoir, likewise for other reservoirs, and has some estimate of the offers made by thermal generators participating in the electricity market.

In respect of inflows, the reservoir manager knows what inflows have occurred in former years, and he knows that there is a degree of correlation in inflows from week to week.

Given this information, and armed with a technique for calculating water values for any particular inflow scenario projected forward, using equation [10], allows him to estimate the water value each week which he also knows will be updated after one week.

The Stochastic Approach

Equation [10] was derived using the assumption of deterministic inflows. But inflows are not deterministic. At any given week, t, the reservoir manager can envisage a large range of possible inflow scenarios which, when each is offered at constant water value, will each end up with a different storage value Sⁱ_t+1 at week t + 1, where i indexes the inflow scenarios from 1 to the total number of inflow scenarios considered possible.

At the end of the week, at time t + 1, each inflow scenario will take storage to a point which, in general, will have a different water value to the water value at time t. Water value is a function of time of year and storage, so let us first assume that the water values are known as a function of storage at time t, so that the final water value for each inflow scenario can be calculated.

Then using our weekly time base, and noting that the water value must give us the expected value of release at time t, the water value at St must be the weighted average of the water values given by the Sⁱ_t+1, given by:

[11]

where p(i, t + 1) is the probability (In EMarket it is assumed that all inflow scenarios are equally likely – more on this in section 6.1.) of inflow scenario i and MWVⁱ_t is the marginal water value calculated for inflow scenario i.

Figure 5 - Weekly Projections of Storage

This is the basic approach used in the RESOP module of the SPECTRA model developed by ECNZ to calculate optimised operating guidelines. RESOP finds the water value contours which have the value of the offers of the major thermal generators. RESOP was developed on the basis of using the marginal costs of the major thermal generators and the original objective of the hydro water value optimisation was to minimise the total annual fuel burn.

However, the basic result in [5] is the same whether the objective is to maximise hydro revenues over all inflow scenarios, or to minimise the cost of the total annual fuel burn over all thermal stations. This means that RESOP can be used in a competitive market environment by substituting actual or estimated thermal offers for costs. Likewise, EMarket will minimise fuel burn when thermal offers reflect fuel and other short-run marginal costs.

Adding Security

Security of supply is of paramount concern in New Zealand’s hydro dominated electricity system. But an inherent weakness of models like RESOP, which project inflows one week ahead at a time, is that they do not take account of the need to prevent the reservoir running dry in a period when inflows are low for weeks or months at a time. This is due to the fact that inflow scenarios are projected no further ahead than the end of the current week, whereas in reality hydro shortage situations develop over a period of many weeks or months.

The starting position of the water value contours in RESOP, i.e. the positions at week 52, are assumed on the first pass through the water value calculation algorithm, and so the optmisation proceeds backward in time to week 1. When the positions are known at week 1, the start of the year, these are then used as the positions at week 52 on the second pass through, and so on until the positions at all weeks converge, which usually occurs on the second or third iteration at most. Security of supply does not figure in the process described above.

In RESOP, achieving adequate security of supply is a protracted process which requires the user to produce a set of water value contours, simulate the market, determine if dry year security was achieved or not, and then adjust the offers or costs of “non-supply” generators – fictional generators added to the simulation to represent the cost of non-supply – until the required level of security is achieved.

One of EMarket’s many strengths is that dry year security of supply is built into the water value optimisation algorithm, eliminating the need to repeat time consuming reruns with different values for the shortage cost or offers for non-supply generation, to achieve the desired level of dry year security.

Figure 6 - Forward Projection of Storage

In order to determine the marginal water value for all values of storage, given any specified 1 in N dry year security constraint, it can first be observed that the marginal water value for an over-full reservoir is no greater than zero (Section 9.4 explains a recent enhancement which allows EMarket to work with spill penalties, in which case the value of water in an already full reservoir may be set less than zero). This is not to say that a generator can not spill at a price above zero, e.g. to keep the price up and maximise revenue by reducing output, which might typically occur when a reservoir is nearing full. The point here is that when the reservoir is already totally full then the marginal value of another cubic meter of water flowing into the reservoir is zero.

The marginal water value for an empty reservoir is harder to define, but when a reservoir is empty the value of an extra 1 MWh of generation, as an equivalent volume in storage, should be at least the nodal price that would occur if the hydro system's generation was removed from the market. The final marginal water value for an empty reservoir can be expressed as a shortage cost, C_S. The implied shortage cost for a reservoir in EMarket is calculated internally from the average nodal price, , for the year for the reservoir and its security factor, the number N from our 1 in N expression of the dry year security criterion. We define the shortage cost used in EMarket by:

[12]

Shortage cost tends to be poorly defined in any model that attempts to simulate it, and estimates of shortage cost vary widely. Shortage in New Zealand during dry years is partly triggered by price (e.g. large industrials with exposure to the spot price reduce production) and partly absorbed by conservation campaigns, and therefore has yet to be demonstrated in a well defined and measurable sense. EMarket’s water value calculations get around this problem by choosing water values that result in a 1 in N chance of shortage starting from the average price contour, where the user has the choice of N, the security factor. The value N is better defined than a shortage cost as 1 in N security has been a stated aim of reservoir management in the past and continues to be relevant today. Since at any point on the average price water value contour the possibility of meeting a shortage situation with the marginal water storage is 1 in N, what EMarket is doing is equivalent to simulating an shortage cost.

In essence, the shortage cost in EMarket is endogenous rather than exogenous, which is a key advantage of this algorithm, in terms of internal consistency, speed and convenience.

Of course, the user can choose to add (and usually does add) non-supply generators at strategic points on the grid. The size and price of these generators does have an impact on the implied shortage cost (and hence on ) although most of the time it is fairly small. Most users will choose the prices on their non-supply generation to act as a flag that non-supply has occurred and perhaps also to be some proxy for an exogenous shortage cost. But their choice is also likely to be made to give spot prices in the event of a very dry year which represent where they believe the market might actually go during such an event.

Given a marginal water value at any time of year, a projection of future dispatches and inflows can be made using forecast demand (Note that EMarket does not model demand elasticity in the forward simulation phase), offers from other generators and the input inflow scenarios. A different projection will be made for each inflow scenario. For a given starting storage, and its water value, a certain number of these projections will eventually reach maximum storage and the others will eventually hit the bottom of the reservoir - this typically happens within just a few months in New Zealand’s storage reservoirs. Since optimal releases are based on a constant marginal water value in between the two storage limits, the average resulting value of the marginal water should be equal to the starting marginal water value. This is the criterion used by EMarket for determining marginal water value's.

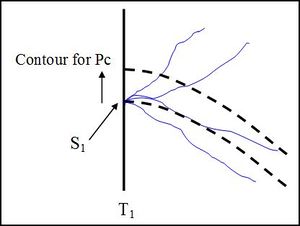
The figure below illustrates how this works, though it must be noted that EMarket does not use this method of projecting storage forward to actually calculate the water value contours – the method is described in section 6. The figure shows storage versus time of year starting from time T₁ and projecting forward for a number of annual inflow scenarios. The dashed black lines are water value contours, and storage at T₁ is equal to S₁ which is on a water value contour. The thin solid traces are the result of dispatching forward with the different inflow scenarios. Most inflow scenarios meet one or other storage constraints within a few months.

Every inflow scenario that hits the top of the reservoir, resulting in spill, must have had a marginal water value of zero, given our result that constant marginal water value is optimal - refer equation [10]. Every inflow scenario that hits the bottom of the reservoir, resulting in shortage, must have had a marginal water value of the shortage cost, C_S. If n inflows scenarios hit bottom then the marginal water value at S₁ is given by:

[13]

where F is the number of annual inflow scenarios entered into EMarket.

Thus, the marginal water value at S1 is equal to the average of the marginal water values of all inflow scenarios at their respective end points at either maximum or minimum storage. The position of the contour at time T₁ is obtained by adjusting the contour position until the average water value over all inflows is equal to the price of the contour. Note that all F inflow scenarios will hit either the top or bottom of the reservoir, usually within a few months.

To illustrate how the water value contours behave, suppose that water value contours for a major hydro system have been calculated for a particular simulation run and at the point at S₁ and T₁ is as shown in Figure 6. Now suppose that the demand input for the run are changed so that demand for the same run is now higher than previously – what happens to the water value contours?

Projecting forward from S1 with higher demand, all other things being equal, will most likely result in greater dispatch of the hydro system. Hence one or more of the inflow scenarios that previously hit the top of the reservoir before hitting bottom will now hit bottom first - let us suppose that just one inflow scenario is affected in this way. As a result, equation [13] will give us . The contours are chosen to have values which are equal to thermal offers set up in the simulation run, so with the lower demand we must have had that MWV = P_c, where P_c is the offer price associated with the contour.

But our new water value is higher than it was previously so our point S₁ at T₁ can no longer be on the water value contour for P_c, since P_c has not changed – only demand has changed in this example. The point at S₁ and T₁ shown in Figure 7 now has a water value greater than P_c, so the water value contour for P_c has moved up at time T₁.

This example shows that increasing demand will tend to move water value contours up relative to storage, though the amount depends on a number of factors in each case. With a little practice, users can also learn to quickly “read” water value contours and predict changes to water value contours.

While this section has illustrated how EMarket calculates water values, the calculations are not actually done in this way, and a shortage cost does not need to be calculated, though the end result is the same. An advantage of using projections that hit either the top or the bottom of the reservoir is the ability to include the 1-in-N security criterion directly in the calculation of water values. This method also captures the full impact of serial correlations within inflows.