Water Values in the EMarket Model

Water Values Defined

The concept of a water value is useful to an owner of some hydro electric generation which has some storage because it tells the owner exactly how much the next MWh of generation is worth at any point in time. Knowing this, the owner could offer their hydro generation into a spot market, for example.

Alternatively, if the owner operated an entire utility which had both hydro and thermal plant, then they could establish a place for the hydro in their "merit order", more simply the order in which the plant should be dispatched given its marginal cost of generation. The assumption here is, of course, that cheaper plant has more merit than expensive plant and should therefore be dispatched first.

The marginal cost of thermal plant is made up of fuel and other variable costs of generation. Hydro electric plant has either small or negligible marginal costs, so the water value is effectively an opportunity cost of operation – this occurs because a MWh of hydro electricity can, in principle, displace a MWh of thermal generation.

Two key characteristics of hydro electric schemes tightly govern what the owner may do with the scheme. One is that storage is limited and the other is that inflows are finite. Hydro generators have strictly limited supplies of water with which to generate.

Consequently, at any particular point in time, the hydro owner must decide if they use water in storage to generate now, or store it longer to use later. Thus the water value can be thought of as the expected future value of water in storage. The hydro owner should take the opportunity to generate whenever the nodal price received for generation is equal to or exceeds the water value.

Although we talk of water value, more correctly we should refer to marginal water value, which is defined as the expected future value of the next cubic meter of water arriving as storage for generation. This implies that the water value should be expressed, for example, in dollars per cubic meter of water. In practice, however, it is more convenient to express it in $/MWh.

Water Value Contours

Figure 1 - Huntly Operating Guideline

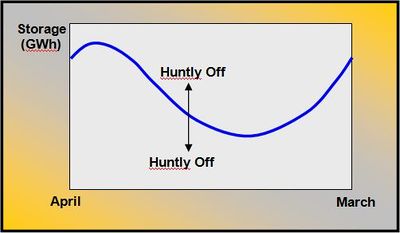
The useful concept of the "operating guideline" arose from the development of various models for ECNZ in New Zealand. An operating guideline is a curve on a chart of total storage for the reservoir in question versus time. The guideline establishes the hydro generator's place in the merit order at any given time of the year.

For example, the Huntly operating guideline shown, for any given time of year, the storage level at which Huntly should be operating, assuming a centrally planned system. At any time during the year Huntly should operate if storage is at or below the thick black operating guideline. In practice, Huntly actually would come on progressively over a range of storage around the guideline. In addition, ECNZ's models calculated guidelines for all major thermal plant based on storage in the two islands.

Figure 2 - Waitaki Water Value Example

Another way to think of the operating guideline is a curve joining points of equal water value – in this case the value of generation from Huntly. Thus, by definition, an operating guideline is a (marginal) water value contour. In designing EMarket, Energy Link decided to continue with the concept of an operating guideline because it is a useful way of visualizing how water value changes with storage and time.

The chart to the left shows typical water value contours for water in the big storage lakes of the Waitaki hydro electric system, Lakes Pukaki and Tekapo, as produced by EMarket. Each contour relates to the offer band from a thermal generator modeled in EMarket. At any given time in the year, if storage is exactly on a contour then it is obvious what it's water value is. If storage is between two contours then the water value is linearly interpolated between the two contours. For example, if storage is one third of the way between two contours of $50/MWh contour and $75/MWh, respectively, then the water value is simply

2/3 x 50 + 1/3 x 75 = $58.33 / MWh

Water Value Theory

Water value contours arise from the process of optimising the use of water in storage lakes, typically upstream of one or more hydro power stations. In fact, the water value contours in EMarket allow the (simulated) hydro owner to calculate water values and simulated offers that are optimal, in a convenient way.

The optimisation of a hydro generation scheme with seasonal storage is different to the optimisation of a thermal generator for three main reasons:

1. the "fuel supply," ie total inflows, is finite in any given year;
2. inflows are highly volatile;
3. storage is finite.

By contrast, thermal generators usually (but not always) have access to unlimited amounts of fuel on call, albeit at perhaps widely varying prices, which can be stored by suppliers in many locations. The three extra restrictions on hydro generators make the optimisation of a hydro system with seasonal storage more difficult and more interesting than operating a thermal generator.

There is one further constraint on hydro generation which is particularly important in New Zealand, where storage is relatively small compared to total inflows. The constraint is known as the "1-in-N" dry year security criteria, where N is in years. For example, the government's policy statement on electricity includes a 1-in-60 security criteria for dry year security of supply. In principle, this means that a shortage situation, in which demand curtailment becomes necessary or desirable, should only occur 1 year in 60 on average. The 1-in-N constraint is included in EMarket's water value calculations for each of the four major hydro systems modeled in EMarket. The four major hydro systems listed below are actually modeled in some detail.

Waitaki

Major storage lakes Pukaki and Tekapo; inflows into lakes Pukaki, Tekapo, Ohau, and the Ahuriri River; eight power stations some with smaller storage lakes immediately upstream.

Clutha

Major storage Lake Hawea; uncontrolled storage and inflows into lakes Wanaka and Wakatipu; other inflows from the Shotover River; Clyde and Roxburgh power stations each with small storage upstream.

Waikato

Lake Taupo with major inflows; eight power stations, each with small storage upstream, modeled downstream, of Taupo; five tributaries inflows modeled below Taupo.

Manapouri

Partially controlled storage Lakes Manapouri and Te Anau; power station at West Arm of Manapouri; outflows also down the Mararoa River.

At this point we resort to some simple maths, but only for a while, and ask the question - if a hydro station has operated for one year from time T₁, at which point it started out with storage of S₁, until time T₂ and storage of S₂, then what would have been its optimal set of releases at each point in the year?

We use the term release to refer only to water released from storage to generate electricity, any other water leaving storage being classed as spill past one or more stations. In the following we make the assumption that generation is a constant function of release. In fact, generation in MW is related to release in cumecs by a number that is approximately constant for most power stations, at least over a wide range of output.

The time step used to calculate the water values is typically one week, so at some week t between T₁ and T₂ the revenue from release is given by:

R_t = P_t x r_t

where P_t is the generator's average weekly nodal spot price at time t. Total revenue for the year is given by:

for all weeks between T₁ and T₂

Marginal costs for hydro electric stations are very low, so if a hydro owner wishes to optimise gross profit over the year then they can just as easily optimise the revenue function R_tot.