Dispatch, Pricing and Power Flows
Disclaimer Reasonable care has been taken to ensure that the information in this paper is up to date at the time of issue. Potential users of EMarket should, however, ensure that they evaluate EMarket and this paper through an appropriate evaluation process in consultation with Energy Link. The authors are also reliant on certain information external to EMarket and Energy Link, for which no liability or responsibility can be accepted.
Introduction
This technical bulletin is intended to provide users and interested parties with a detailed explanation of how EMarket’s IQP dispatch and pricing module functions, including the DC power flow calculations embedded within it.
Other Documents
This bulletin is one of a series of technical bulletins relating to Energy Link’s EMarket and EMarketOffer (EMO) models. Taken together, the bulletins replace the old EMarket User Guide. A full series of bulletins covers an overview of the EMarket model, the details of the four major New Zealand hydro systems modelled in EMarket, water values and hydro offers, power flows, dispatch and nodal pricing, short term river chain optimisation and company optimisation.
Dispatch
Dispatch and pricing in EMarket and EMO are primarily determined by the methodology specified in Schedule 1 of Part 2 of the New Zealand Electricity Governance Rules (EGRs). The market implementation of these methodologies is currently Trans Power's SPD model which is a large scale LP.
Reserves modelling is required within EMarket, primarily due to their impact on generation. The reserve constraints are straight forward to model in principle, however, a major concern with reserves is the large number of reserve constraints which combine to significantly increase the processing time, often for little or no additional accuracy.
RiskOffsets are also required for the modelling of reserves. These are calculated for SPD using TransPower's RMT tool which is a complex non linear dynamic model of the generation and load on the Grid. RMT is too complex to implement within EMarket.
In EMarket and EMO dispatch, pricing and power flow are achieved by Energy Link’s IQP software module.
Optimum Dispatch
The dispatch objective function from Schedule G6 of Part G of the EGRs is to maximise the net purchaser surplus.
EGR Dispatch Objective
where the Di are the demand bids and the BPi the bid prices, Gj the dispatched generation with offers OPj, Rk the dispatched reserves with offers ORk.
This objective function is used to form the forecast prices and the pre-dispatch schedule using the demand bids BPi, generator offers OPj and reserve offers ORk. But provisional and final prices are calculated using metered demand, so in effect it is performed by minimising the Cost function shown below. Note that the offers Ox have units of $/MWh whereas G and R have units of MW, so Cost has units of $/hour.
Pricing Objective Function
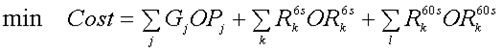Both objective functions are subject to the constraints listed in the following table (This is not a complete list of all of the constraints within SPD). Note that j indexes generators, i indexes either lines or island, depending on context, n indexes nodes and c indexes class of reserve.
| Constraint | Formulation |
|---|---|
| Generator output greater than zero | Gj ≥ 0 ∀j |
| Generator output less than maximum output | Gj - Gj,max ≤ 0 ∀j |
| Generation plus reserve less than generator's maximum output | Gj +Rj - Gj, max ≤ 0 ∀j |
| Reserve less than a specified input, rslopej, proportion of generation | Rj - rslopejGj ≤ 0 ∀j |
| Nodal Energy Balance Constraints: Energy conserved at each and every node. Note that the Zin and Zout include any HVDC flows in or out of node | 
|
| AC line flow, Zi, within thermal limits which are usually the same in both directions | Zi - Zi, max ≤ 0 ∀j Zi, min - Zi ≤ 0 ∀j |
| HVDC MW within limits but note maximum transfer different in each direction | As for AC lines |
| Losses match power flows | Handled by DC power flow formulation |
| Island Reserve Constraints: For each island and class of reserve (6s and 60s) total reserves greater than or equal to island risk Si | 
|
| For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times maximum generator unit output less RiskOffset | Si, c ≥ IRAFi, c max (Gj - RiskOffset) |
| For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times HVDC MW into island less HVDC overload factor ZDCOL for the island | Si, c ≥ IRAFi, c (ZDC - ZDCOL) |
| For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times island minimum risk | Si, c ≥ IRAFi, c Smin, i, c |
| Security constraints - we understand these are not usually in use | n/a |
| Ramping – ability of generators to achieve new output within a half hour | n/a |
The calculation of the island reserve risk in EMarket includes the minimum island risk entered by the user, so hydro risk in the South Island is covered.
The IQP Dispatch Algorithm
IQP, our iterated quadratic program, was developed solely by Energy Link to find optimal dispatches of generation and reserve. Quadratic programming is a widely used optimisation technique and avoids many of the pitfalls that can occur in more general problems, particularly if the objective function is convex.
Formulation of the Optimisation Problem
IQP is used to find an optimum solution for dispatching generation on the grid based on a set of generation and reserve offers, fixed nodal demand, and a large set of constraints including line limits and reserves constraints.
The value of the objective function will henceforth be referred to as the Cost of a dispatch, or Cost(d) and the object of a dispatch to minimise Cost(d).
The generation must equal the demand across the grid including losses. This condition can be expressed as the Global Conservation of Energy Constraint.
Global Conservation of Energy Constraint
where DTot is the figure for total demand and L is the total losses on the grid (L includes the losses on the Grid between GIPs and GXPs. It does not include distribution losses that are incurred downstream of each GXP).
Losses can be calculated from net nodal injection, where net injection at a node is the difference between injection and off-take at the node. IQP uses the standard DC power flow formulation where one node is designated the swing node or swing bus. Net nodal generation at the swing node balances the total net generation of all other nodes to satisfy the global conservation of energy constraint.
Losses in a DC Power Flow
: i,j = 0 to N - 1