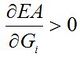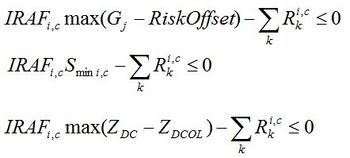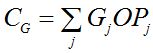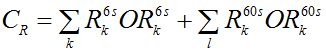Dispatch, Pricing and Power Flows

Disclaimer Reasonable care has been taken to ensure that the information in this paper is up to date at the time of issue. Potential users of EMarket should, however, ensure that they evaluate EMarket and this paper through an appropriate evaluation process in consultation with Energy Link. The authors are also reliant on certain information external to EMarket and Energy Link, for which no liability or responsibility can be accepted.

Introduction

This technical bulletin is intended to provide users and interested parties with a detailed explanation of how EMarket’s IQP dispatch and pricing module functions, including the DC power flow calculations embedded within it.

Dispatch

Dispatch and pricing in EMarket and EMO are primarily determined by the methodology specified in Schedule 1 of Part 2 of the New Zealand Electricity Governance Rules (EGRs). The market implementation of these methodologies is currently Trans Power's SPD model which is a large scale LP.

Reserves modelling is required within EMarket, primarily due to their impact on generation. The reserve constraints are straight forward to model in principle, however, a major concern with reserves is the large number of reserve constraints which combine to significantly increase the processing time, often for little or no additional accuracy.

RiskOffsets are also required for the modelling of reserves. These are calculated for SPD using TransPower's RMT tool which is a complex non linear dynamic model of the generation and load on the Grid. RMT is too complex to implement within EMarket.

In EMarket and EMO dispatch, pricing and power flow are achieved by Energy Link’s IQP software module.

Optimum Dispatch

The dispatch objective function from Schedule G6 of Part G of the EGRs is to maximise the net purchaser surplus.

EGR Dispatch Objective

where the D_i are the demand bids and the BP_i the bid prices, G_j the dispatched generation with offers OP_j, R_k the dispatched reserves with offers OR_k.

This objective function is used to form the forecast prices and the pre-dispatch schedule using the demand bids BP_i, generator offers OP_j and reserve offers OR_k. But provisional and final prices are calculated using metered demand, so in effect it is performed by minimising the Cost function shown below. Note that the offers Ox have units of $/MWh whereas G and R have units of MW, so Cost has units of $/hour.

Pricing Objective Function

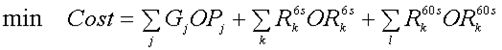Both objective functions are subject to the constraints listed in the following table (This is not a complete list of all of the constraints within SPD). Note that j indexes generators, i indexes either lines or island, depending on context, n indexes nodes and c indexes class of reserve.

Constraint	Formulation
Generator output greater than zero	G_j ≥ 0 ∀j
Generator output less than maximum output	G_j - G_j,max ≤ 0 ∀j
Generation plus reserve less than generator's maximum output	G_j +R_j - G_{j, max} ≤ 0 ∀j
Reserve less than a specified input, rslope_j, proportion of generation	R_j - rslope_jG_j ≤ 0 ∀j
Nodal Energy Balance Constraints: Energy conserved at each and every node. Note that the Z_in and Z_out include any HVDC flows in or out of node
AC line flow, Z_i, within thermal limits which are usually the same in both directions	Z_i - Z_{i, max} ≤ 0 ∀j Z_{i, min} - Z_i ≤ 0 ∀j
HVDC MW within limits but note maximum transfer different in each direction	As for AC lines
Losses match power flows	Handled by DC power flow formulation
Island Reserve Constraints: For each island and class of reserve (6s and 60s) total reserves greater than or equal to island risk S_i
For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times maximum generator unit output less RiskOffset	S_{i, c} ≥ IRAF_{i, c} max (G_j - RiskOffset)
For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times HVDC MW into island less HVDC overload factor Z_DCOL for the island	S_{i, c} ≥ IRAF_{i, c} (Z_DC - Z_DCOL)
For each island and class of reserve (6s and 60s) island risk greater than or equal to island risk adjustment factor times island minimum risk	S_{i, c} ≥ IRAF_{i, c} S_{min, i, c}
Security constraints - we understand these are not usually in use	n/a
Ramping – ability of generators to achieve new output within a half hour	n/a

The calculation of the island reserve risk in EMarket includes the minimum island risk entered by the user, so hydro risk in the South Island is covered.

The IQP Dispatch Algorithm

IQP, our iterated quadratic program, was developed solely by Energy Link to find optimal dispatches of generation and reserve. Quadratic programming is a widely used optimisation technique and avoids many of the pitfalls that can occur in more general problems, particularly if the objective function is convex.

Formulation of the Optimisation Problem

IQP is used to find an optimum solution for dispatching generation on the grid based on a set of generation and reserve offers, fixed nodal demand, and a large set of constraints including line limits and reserves constraints.

The value of the objective function will henceforth be referred to as the Cost of a dispatch, or Cost(d) and the object of a dispatch to minimise Cost(d).

The generation must equal the demand across the grid including losses. This condition can be expressed as the Global Conservation of Energy Constraint.

Global Conservation of Energy Constraint

where D_Tot is the figure for total demand and L is the total losses on the grid (L includes the losses on the Grid between GIPs and GXPs. It does not include distribution losses that are incurred downstream of each GXP).

Losses can be calculated from net nodal injection, where net injection at a node is the difference between injection and off-take at the node. IQP uses the standard DC power flow formulation where one node is designated the swing node or swing bus. Net nodal generation at the swing node balances the total net generation of all other nodes to satisfy the global conservation of energy constraint.

Losses in a DC Power Flow

: i,j = 0 to N - 1

where N is the total number of nodes and the y_i are the net nodal injections, i.e. y_i is the total generation at node i minus total demand at node i minus distributed losses. B is the susceptance matrix for the Grid, where the susceptance is approximately the reciprocal of the line reactance.

Since y_i is a linear function of G_i, the global conservation constraint can be transformed into a general quadratic form.

General Form of the Global Conservation of Energy Constraint

where α_ij is a matrix of constant coefficients, β_i a column vector of constant coefficients and δ is the total demand D_Tot. The first term is quadratic in G_j and is the losses term. The second term is linear in G_j and is the generation term.

The other constraints on the power flows are the line limits. Power flows through transmission lines are given as part of the DC power flow equations and these are constrained to lie within maximum and minimum flow limits.

Line Constraints

H is called the transfer admittance matrix for the Grid.

Total reserve constraints for each region are:

Reserves Constraints

: i ∈ I

where I is the set of reserve offers in an island and G_i is a significant generation dispatch in that region.

PLSR Reserve Constraints

R_i < rslope_iG_i , R_i < G_{max, i} - G_i

where PLSR reserve offer i is associated with generation offer j and rslope_j is the maximum reserve that can be provided as a proportion of generation G_j.

Apart from the general form of the global conservation of energy constraint (see section 3 2.1.3 on page 4), all constraints are linear. While the problem is in this form it can only be described as a general optimisation problem. It is unclear even whether the problem is convex or if it has a single local minimum. It can be demonstrated however that it has a single local minimum under certain conditions (An important condition is that negative offers are not on the margin. Negative offers are not currently permitted under the EGRs) and also that these conditions can be used to formulate our particular problem of optimising the dispatch of generation on the grid.

One difficulty to overcome is the presence of zero price offers: if a combination of these can satisfy all conditions then the solution is degenerate (Degenerate simply means that there is more than one dispatch that satisfies the conditions that the Cost objective function is minimised. In this case the minimum Cost is zero). It is necessary to make an arbitrary decision in this case and IQP actually assigns a price of $0.01/MWh to all zero offers. This is also consistent with the EGRs which prevent degeneracy through the Must-run Dispatch Auction in which generators bid for the right to offer zero, but only up to a major portion of total demand.

Now we can make some assumptions about the energy available to be dispatched.

Available Energy

EA is a variable representing available energy. This somewhat arbitrary value is the total demand that could be satisfied by a dispatch of plant if net injection at the swing bus was adjusted to make EA equal to total demand.

Since losses are only a small fraction of generation for all realistic situations we can make an assumption for the partial derivative of EA.

Partial Derivative of the Available Energy

Given that no negative price offers are included, we can replace the pricing objective function (on page 2) with an inequality constraint.

Available Energy Constraint

EA ≥ D_Tot

The partial derivative shows that EA can always be reduced by reducing generation, which in turn can be achieved at a lower or equal Cost. So for any dispatch satisfying the available energy constraint there can always be found one with less or equal cost that satisfies the global conservation of energy constraint (on page 3). This means a minimal solution to the problem with the global conservation of energy constraint, will also be a minimal solution to the problem with the available energy constraint.

If Γ(E) is defined as the set of dispatches where EA(d) ≥ E and which also satisfy all the linear constraints, then the optimisation process can now be stated as:

Problem 1: minimise (Cost(d)) where d ∈ Γ(D_Tot).

A set π(P) can be defined as the set of dispatches that satisfy all the linear constraints and Cost(d) ≤ P. Since Cost is a linear function of the dispatch variables, this set is entirely defined by linear constraints. The maximisation problem:

Problem 2: maximise (EA(d)) where d ∈ π(P)

Is a member of the quadratic programming family since it involves only linear constraints and has a quadratic objective function. Furthermore EA(d) is a convex function so any local maxima of this problem will also be a global maxima.

It can be shown that if d1_Opt is a solution to Problem 1 and d2_Opt is a solution to:

Problem 2a: maximise(EA(d)) where d ∈ π(P_s) and P_s = Cost(d1_Opt)

then d2_Opt is also a solution to Problem 1.

This can be shown:

Firstly, it is true that d1_Opt ∈ π(P_s) since Cost(d1_Opt) = P_s.

Therefore EA(d2_Opt) >= EA(d1_Opt) and this means that d2_Opt ∈ Γ(D_Tot)

Since Cost(d2_Opt) ≤ P_s, the cost of an optimal solution to Problem 1, d2_Opt must also be an optimal solution to Problem 1.

The Iteration Process

We found above we can solve Problem 1 by:

finding the cost of the optimal dispatch, P_s
then solving the quadratic programming problem, Problem 2.

This is done in the IQP algorithm by first making an educated guess for a value for P, then solving Problem 2 and using the EA_max of the solution to re-estimate P, repeating until a solution is found with an EA_max = D_Tot. It usually takes only two or three iterations in order to find a very good estimate of P_s.

Figure 1 - Available Energy as a Function of Cost

One by-product of the optimisation of Problem 2 is the Lagrange multiplier for the cost constraint which is the inverse of 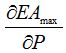. This allows a new figure of P to be estimated by the Newton method which gives convergence on a solution for P_s very quickly.

Figure 1 illustrates a typical 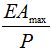curve. In this case there is an infeasible region to the left caused by the northward constraint on the HVDC link (The DC equations balance the demand in the North Island with generation from the swing node, which in this example is in the South Island, causing a high northward flow when dispatched generation is low).

The point where EA_max meets the Total Demand line, D_Tot, is the solution point. Since the curve has a smoothly decreasing slope toward higher values, the Newton method works well from a first estimate of P that is not too much greater than P_s.

To deal with overshoots that are a feature of using the Newton method the algorithm keeps a track of a low P value and a high P value and uses the bisection method if these limits are exceeded by the Newton method. If a solution is first found infeasible then P is increased until either a solution is found or the whole problem is declared infeasible.

Convergence and Accuracy of IQP

The iteration process continues until convergence is obtained, i.e. until the available energy, equal to total generation less the total losses, is within 0.0001 MW of the required demand, which typically occurs within 3 to 5 iterations.

If the IQP algorithm fails to converge quickly to this value then it switches to a modified bisection method which generally converges. If a dispatch is ultimately infeasible then IQP returns an error code 1, indicating a no solution error.

IQP can correctly produce negative prices, but will not accept negative offers. Zero offers are set to $0.01/MWh so if there is enough low priced generation to satisfy demand plus losses, then the losses determine the dispatch.

Inclusion of Losses

Figure 2 - Modelling of Losses

A DC power flow (on page 10) does not include losses in the flows calculated in each line of the Grid, but the losses can easily be calculated separately. Losses are therefore included in dispatch for each line by calculating the line loss on the line and adding these to the demand at the node at the receiving end of the line, as occurs in SPD.

In the figure to the right the dark arrow at the receiving node shows the actual demand. The lighter arrow shows the demand including actual demand plus the line losses on this line.

After IQP is run once with nil distributed losses, the line losses are recalculated and the dispatch is recalculated.

Nodal Pricing

Nodal energy prices are the shadow prices of the nodal energy balance constraints applied in SPD and the island reserve prices are the shadow prices of the island reserve constraints applied in SPD.

The shadow price of a constraint is the change in the optimum Cost when the constraint is relaxed by one unit. To calculate the shadow price re-optimisation is required when the constraint is relaxed, so shadow prices must not be confused with the change in Cost from a simple change in generation by 1 MW at a node.

In IQP, the shadow prices are available as Lagrange multipliers on the appropriate constraints.

Note that the EGRs also specify that a DC power flow (on page 10) is to be used when dispatching and calculating prices. This is a power flow that makes simplifying assumptions about the relationship of the reactance and resistance of each line and also doesn't calculate the losses on each line.

SPD is a large scale LP and its DC power flow is incorporated directly into the LP formulation. The more traditional approach is to use a separate DC power flow and a non-linear program, as occurs within IQP.

A standard DC power flow calculates very quickly and implicitly achieves global energy balance at all nodes except perhaps at the "swing bus." IQP therefore does without the many nodal energy balance constraints within SPD and uses only the one global conservation of energy constraint:

where L is the total losses on the Grid.

With only one energy constraint however, IQP requires formulae that calculate the desired nodal energy prices from the Lagrange multiplier of the global conservation of energy constraint and other Lagrange multipliers that are available from IQP. The following derivation shows how this is achieved.

In addition to aggregating the nodal energy balance constraints into a global conservation of energy constraint, combine the reserve and risk constraints as follows:

The IRAFs are now almost always equal to 1. Form the Lagrangian function where

is the cost component due to generation and

is the cost component due to reserves.